Abstract
Background In the lumbar spinal column, an annular disruption may be sealed after annulotomy to prevent further prolapse and instability. We investigated the biomechanical effects of various material properties of an injectable sealant
Methods We used a 3-dimensional, nonlinear, osteoligamentous, experimentally validated finite-element model of the L3–L5 spine segment to study annulotomies of varying sizes and locations in the L3–L4 annulus followed by replacement with isotropic sealants (plugs) with a Young's modulus of 0.4, 2.0, 4.0, 6.0, and 40.0 MPa. Annulotomies in the region of the posterior longitudinal ligament were studied with and without the ligament in place. Intact, destabilized, and repaired models were subjected to 400 N compression and 12.7 Nm moment in all loading modes to compute plug forces, plug stresses, motion characteristics, and annulus bulge.
Results Changes in sealant stiffness minimally affected the overall motion characteristics of the segment. Increases in shear stress and von Mises stress were proportional to the stiffness of the sealant. The von Mises stress was inversely proportional to plug size. Removal of portions of the posterior longitudinal ligament did not significantly alter motion between spinal segments or stress in the annulus fibrosus. Removal of portions of the ligament increased the disc bulge when plugs were less stiff. Intradiscal pressure decreased when an annulotomy was created. The sealant generally restored nucleus pressure to a degree proportionate to sealant stiffness.
Conclusions Minimizing sealant stresses as well as expulsion and separation forces should lead to a minimal Young's modulus. Sealant materials with a Young's modulus close to 6 MPa are most appropriate. The allowable variation in material properties is reduced with increased annulotomy size. Removal of posterior longitudinal ligament only allows increased sealant bulge when the sealant's modulus of elasticity is very low. This removal does not affect spinal unit biomechanics or annulus stress in annulotomy or annulotomy with sealant repair.
INTRODUCTION
Two different approaches are in use for treatment of lumbar herniation, conservative and surgical.1–6 Surgery is considered after failure of conservative treatment. Partial discectomy is one of the most commonly implemented surgical spine procedures. The immediate postoperative satisfaction of the patient after a primary discectomy is often cited as relatively high, but recent reviews have suggested that patient satisfaction and return-to- normal-activity measures could be low.2 Clinical follow-ups suggest that repeat discectomies, because of recurrent disc herniation, contribute to this poor patient outcome.
The clinical success rate of discectomy may be further enhanced if the rupture can be repaired and/or sealed. Clinically, this would reduce reherniations and further improve the outcome of the first surgery. Biomechanically, it could help restore the load-bearing function of the disc without compromising the motion of the spine. Injecting an elastic material into the rupture created during the limited discectomy (creating a plug) makes it possible to restore the sheet that surrounds the nucleus.7–9 Cauthen et al. have developed a mesh-type sealant for this purpose that is being evaluated in vivo.2
Both the ground substance and the layers of embedded collagenous fibrils influence the material properties of the annulus.10 The stiffness of disc sealant material from which this plug is constructed should match the composite stiffness of the annulus for it to be effective. The stiffness of the annulus changes from person to person, and it is not practical to have sealant materials of varying stiffness for clinical use. The stiffness of the entire disc also changes with age and degeneration. Degenerated discs become more flexible during the initial stages of degeneration and stiffer at the later stage of disc degeneration, compared with a healthy disc.
Our hypothesis was that the material properties of the disc sealant that will restore the segment mechanics are independent of the size and location of the annulotomy, which is an accepted surgical procedure to repair a herniated disc, and of the loading mode. We evaluated the biomechanics of the annulotomy procedure and identified the optimal sealant material stiffness that will best restore the disc biomechanics.
MATERIALS AND METHODS
The ligamentous finite-element model used in this study was previously developed12 and included lumbar vertebrae L3, L4, and L5 and the spinal structures associated within the motion segments. This sagittaly symmetric nonlinear ligamentous model consisted of 13,339 elements and 16,240 nodes. The geometry for the model was created by outlining computed tomography scans at 1.5 mm increments. Each vertebral body consisted of cortical (dense) bone encapsulating a cancellous (porous) core. The discs were defined by the nucleus pulposus in the center and 8 layers of annulus laminates. The laminates were defined with composite elements consisting of fibers as rebar elements oriented at 120° to each other, embedded in ground substance. These fibers were unable to withstand compression. The facet joints between the vertebral bodies were treated as sliding areas of cartilage that were simulated with the GAPUNI command in ABAQUS/Standard version 6.5 (ABAQUS Inc, Providence, RI). The ligaments (interspinous, supraspinous, intertransverse, posterior longitudinal, capsular, anterior longitudinal, and ligamentum flavum) were incorporated as nonlinear elastic truss elements. Our group previously used fresh-frozen cadaver spines to validate this model for motion characteristics under physiological loads.12 Table 1 summarizes the element number, type, and properties used in this model.
Breakdown of Elements in Lumbar L3–L5 Finite Element Model12
A 400 N compressive load distributed across the cranial portion of L3 simulated the static trunk load on the lumbar spine. In addition to simulating bending, we applied a 12.7 Nm moment to beams attached to the upper surface of L3. These moments were applied in flexion, extension, left lateral bending, right lateral bending, left axial rotation, and right axial rotation. All moments were applied independently and were not combined. At the caudal end, L5 was constrained in all 3 translations and in all 3 rotations.
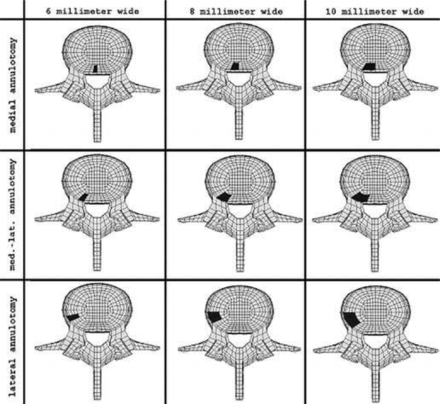
The experimentally validated intact model was altered to create an annulotomy in the left posterior quadrant of the L3-L4 annulus (Figure 1). The rectangular annulotomy extended from the lower to the upper endplate and through the entire annulus. To determine the effect of location on spinal biomechanics, we created the annulotomy in 3 locations, medial (intracanal), medial-lateral (intraforaminal), and lateral (extraforaninal). To establish annulotomy size effects, we simulated annulotomy widths 6 mm, 8 mm, and 10 mm at the annular surface. The annulotomy tapered approximately 5° from the face of the annulus to the nucleus. In the medial annulotomy, any affected posterior longitudinal ligament was removed to mimic surgery.
Superior view of annulotomy locations in the left posterior portion of the annulus in the lumbar L3–L5 model.
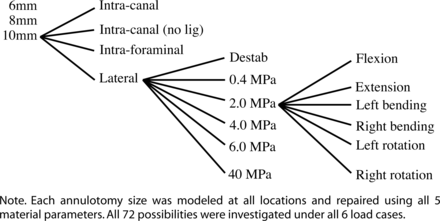
To determine the amount of destabilization that occurred after annulutomy, we computed the rotation across each functional spinal unit for each of the loading conditions. In addition, we computed L3-L4 nucleus pulposus pressure after the annulotomy. To simulate an injectable sealant (plug), we exactly replaced the removed section with a sealant of varying isotropic material properties: a Young's modulus of 0.4 MPa (very weak), 2.0 MPa (weak), 4.0 MPa, 6.0 MPa (stiff), and 40.0 MPa (very stiff). Finally, to determine the contribution of the posterior longitudinal ligament, we reintroduced it to the model in cases with a medial annulotomy. The hierarchy used in this model is shown in Figure 2.
Hierarchy of models simulating an injectable sealant (plug).
To determine the stress within the nucleus pulposus, we measured the average nodal pressure within the L3—L4 nucleus. We also measured the annulus bulge in a vertical plane that cut the sealant into 2 equal halves. The values reported reflect the horizontal distance that the outer nodes of the annulus deflected from a line constructed on the plane between a node on the outer surface of the upper end plate and the outer surface of the lower end plate. Average nodal shear stresses were calculated on the surface of the sealant, and average von Mises stresses were determined within the sealant.
RESULTS
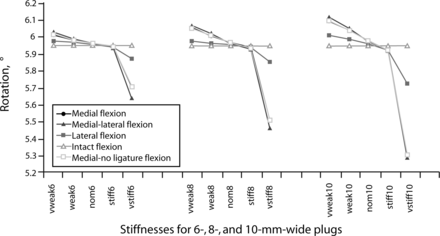
The functional spinal unit motion decreased compared with intact motion when the Young's modulus of the sealant was 6 MPa for all annulotomy sizes and locations. Decreasing this stiffness by 50% in all cases affected the functional unit rotation value by less than 5%. As an example, the rotation under a flexion moment for a 10-mm medial sealant was highest when the sealant was weakest (very weak, 0.4 MPa), with 0.15° of rotation greater than intact. As the sealant stiffness increased, the amount of rotation decreased consistently to 0.02° less than intact when the sealant stiffness was 6 MPa. With the addition of the sealant with stiffness of 40 MPa, there was a 0.64° decrease in motion compared with intact.
Removal of the posterior longitudinal ligament had no significant effect on functional spinal unit rotation. Graphical rotation results for flexion with the sealant are shown in Figure 3.
Rotation across L3–L4 functional spinal unit under 400N compressive load and 12.7 N-m flexion moment, measured in the finite element model with varying annulotomy size and location. In these models, the nucleus has been sealed with materials of varying stiffness.
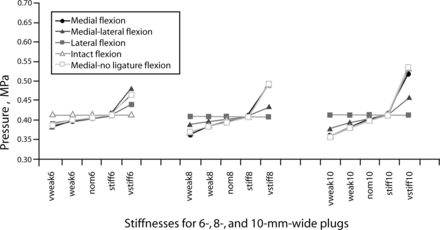
Creating an annulotomy diminished the nucleus pulposus pressure. In general, with increasing sealant material stiffness, nucleus pulposus pressure also increased under physiological loading. This was amplified with larger implants. Under all load cases and all annulotomy sizes, the pressure of the repaired nucleus intersected the pressure of the intact nucleus when the sealant material property was 6 MPa. For instance, the pressure developed in the nucleus from a flexion moment for a 10-mm medial sealant was lowest when the sealant was weakest (0.4 MPa), a 13% pressure drop. As the sealant stiffness increased, the pressure increased consistently to 0.2% less than intact when the sealant stiffness was 6 MPa. With the addition of the sealant with stiffness of 40 MPa, there was a 30% pressure increase compared with intact. With regard to all of the data, decreasing this stiffness by 50% in all cases affected the nucleus pressure value by less than 5%. The flexion nucleus pressure with sealant is shown in Figure 4.
Nucleus pressure in the L3–L4 intervertebral disc under 400N compressive load and 12.7 N-m flexion moment, measured in the finite element model with varying annulotomy size and location. In these models, the nucleus has been sealed with materials of varying stiffness.
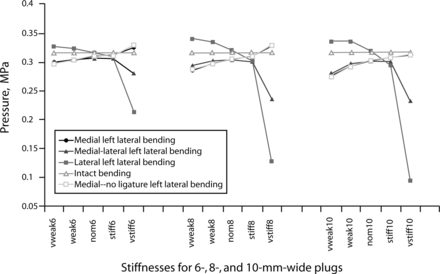
Implants with material stiffness at 40 MPa exhibited nucleus pressure variations that did not necessarily follow this trend. For example, when the 40-MPa implants were placed on the left lateral side and loaded in left lateral bending, the pressure of the nucleus decreased up to 70% (10-mm annulotomy). When these same implants were in tension and in an extreme fiber location, they tended to raise the pressure of the nucleus 63% for the right lateral load case with the left lateral implant. Pressure results for lateral bending with the sealant are shown in Figure 5. Similar trends were seen in the flexion-extension load cases with 10- MPa implants in the medial location.
Nucleus pressure in the L3–L4 intervertebral disc under 400N compressive load and 12.7 N-m left lateral bending moment, measured in the finite element model with varying annulotomy size and location. In these models, the nucleus has been sealed with materials of varying stiffness.
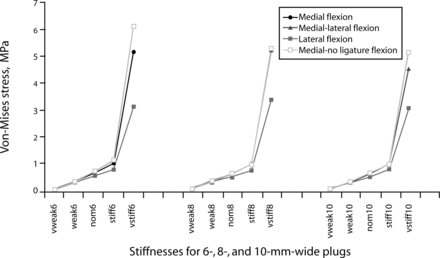
Plug body stresses generally increased with increasing implant stiffness and decreasing implant width. The highest plug stresses were observed in the load case where the plug was located at an extreme fiber location. This effect was minimized with increasing plug size. The removal of the posterior longitudinal ligament had no effect on the von Mises stresses within the plug.
The highest observed stress, 16.45 MPa, occurred in the 6-mm (smallest) plug with a stiffness of 40 MPa (the stiffest) under the left lateral bending load case when the plug was located laterally. The plug stresses were minimized in the axial rotation load case. Von Mises stress results for the sealant are shown in Figure 6.
Von-Mises stress within the injectable sealant used in the L3–L4 intervertebral disc under 400N compressive load and 12.7 N-m flexion moment, measured in the finite element model with varying annulotomy size and location. In these models, the nucleus has been sealed with materials of varying stiffness.
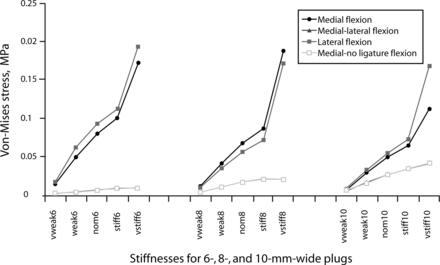
Plug shear stresses also generally increased with increasing plug stiffness but were unaffected by plug width. The greatest plug shear stresses were observed in the load case where the plug was located at the center of rotation for a given load case. The maximum shear stress, 0.246 MPa, for example, occurred when an 8-mm plug was in a medial location and loaded under left lateral bending. Removal of the posterior longitudinal ligament had an insignificant effect on the shear stresses observed in the plug. Plug face shear stress results for the sealant are shown in Figure 7.
Shear stresses on the face of the injectable sealant used in the L3–L4 intervertebral disc under 400N compressive load and 12.7 N-m flexion moment, measured in the finite element model with varying annulotomy size and location. In these models, the nucleus has been sealed with materials of varying stiffness.
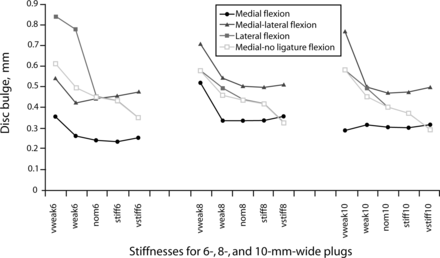
Plug bulge increased with decreasing plug stiffness. The trend was more pronounced with increasing plug size. Bulge was greatest when the plug was located at an extreme fiber location for a load case with a maximum of 1.4 mm past the intact contour when the sealant was in the lateral position and under a left lateral bending moment. Removing the posterior longitudinal ligament affected the amount of plug bulge only for the plugs with 2 MPa and 0.4 MPa. Plug face bulge results for the sealant are shown in Figure 8. For additional results, methodology, and discussion, see Holekamp.13
Maximum bulge on the face of the injectable sealant used in the L3–L4 intervertebral disc under 400N compressive load and 12.7 N-m flexion moment, measured in the finite element model with varying annulotomy size and location. In these models, the nucleus has been sealed with materials of varying stiffness.
DISCUSSION
The annulotomy is an accepted surgical procedure for the herniated disc. Creating an annulotomy makes it possible to reduce the amount that the disc protrudes into the space where the nerve roots are located and thus, to reduce pain. However, some patients are not satisfied with the outcome. Efforts are under way to seal the rupture to prevent reherniation, a root cause of repeat surgeries and the main contributor to poor patient satisfaction.
Our study used an experimentally validated finite-element model, because experimental investigation of this issue is not practical. Experimental study would require previous knowledge of a material that would mechanically interlock into the annulus. To restore disc mechanics, the material properties of such a device would need to vary over a wide range. Each parameter would require testing 5–10 ligamentous functional spine units. An advantage of using the finite-element approach to study the effects of various parameters of a plug design on the biomechanical parameters before undertaking a full-scale experimental study is the limited investment of resources required. Such a study could determine the optimal set of design parameters likely to yield a satisfactory solution in an experimental study.
Repairing the disc with a sealant allows both the nucleus pressure and the functional spinal unit's response to external load to be restored. Our results suggest that a sealant material property of 6 MPa is an appropriate choice for restoring segment biomechanics, including nucleus pulposus pressure and plug bulge back to physiological conditions. Varying the sealant stiffness up to 50% would be minimally detrimental to functional spinal unit stiffness and nucleus pressure. The biomechanical dependence of the spine on the sealant increases with increasing implant size. Therefore, if a suitable material cannot be developed, it might be beneficial to place a maximum allowable width constraint on the annulotomy.
Sealant stresses increase with increasing sealant stiffness and decreasing sealant width. The increase in stress confirms that the sealant participates in load sharing with the nucleus and the remainder of the annulus. As stiffness increases, overall motion of the functional spinal unit is impeded by the implant, and the implant's stress increases. In addition, decreasing the width of the implant causes the cross-sectional area to decrease, and the stress in the implant to increase. Therefore, if the yield strength of a very stiff material is low, the width of the implant may need to be limited to avoid material failure.
Limiting sealant size would also limit sealant bulge, although this is not necessary for sealant stiffness above 6 MPa. In these cases the bulge was less than that of an intact segment and would not be a factor. Sealant bulge was the only parameter for which removal of the posterior longitudinal ligament had any significant implications. When sealant stiffness was very small, the posterior longitudinal ligament seemed to limit bulge. This did not occur when sealant stiffness was more than 4 MPa.
Minimal change in shear stress was observed in relation to size. Shear failure may be the source of poor conditions of the annular-sealant interface. Size and location have minimal impact on shear stresses, so it may be important to change the shape of the implant, possibly to an inverted cone, to help limit expulsion.
The next step toward creating a viable sealant is to evaluate the structural properties of actual materials that have been approved for use in the human body. Because this implant will be subject to fatigue, future work should consider fatigue characteristics and should investigate both the body stresses and the shear stresses of the material. It has been suggested that delamination may be the primary mode of failure of a sealant. To address this possibility, further studies to compute adhesion stresses should be undertaken, and the results compared to adhesion strengths of common polymers. It should be assumed that adhesion failures occur, and a model should be created with an unbound plug to determine the implant's behavior once delamination has occurred. If the geometry of the plug is changed, it may be possible to minimize its migration after failure. Future models should investigate this possibility. Finally, the surgical approach necessary to perform the annulotomy should be considered and incorporated into the model. For example, a facetectomy or laminectomy is usually included in an intraforaminal or an intracanal annulotomy procedure and should be included when considering those annulotomy locations in the model.
In conclusion, we found that bulge and rotational motion across the motion segment increase with increasing annulotomy size and decreasing sealant stiffness. We determined that an optimum isotropic modulus of elasticity for the plug, which would restore normal mechanics to the injured segment, is 6 MPa.
Footnotes
The authors report no conflicts of interest.
No IRB approval was needed for this study.
- Received January 3, 2007.
- Accepted March 5, 2007.
- Copyright SAS - Spine Arthroplasty Society 2007
This is an Open Access article distributed under the terms of the Creative Commons Attribution-Noncommercial 3.0 Unported License, permitting all non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.